【LeetCode 5】Longest Palindromic Substring 最长回文子串

发表于 | 分类于

[LeetCode 5]Longest Palindromic Substring 最长回文子串

问题描述:

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

说明：解集不能包含重复的子集。

示例1:

1
2
3
输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例2：

1
2
输入: "cbbd"
输出: "bb"

Solution:

Solution 1:
之前的考虑，最长回文字符串即字符串与倒置的字符串的最长公共字符串，但是并不正确，考虑acbca；最长公共子字符串dp解法时间复杂度为O(2)，dp[i][j]表示从i到j的最长公共子字符串，字符串p1…..pi,q1…..qj转移方程：i/j=0,dp[i][j]=0;q[i]==p[j],dp[i][j]=dp[i-1][j-1]+1;q[i]!=p[j],dp[i][j]=0;

Code:

wrong
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

int n = s.length();
        String sRevert = new StringBuilder(s).reverse().toString();
        int maxLength = 0;
        int pos = 0;
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0 || j == 0)
                    dp[i][j] = 0;
                else if (s.charAt(i - 1) == sRevert.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    maxLength = Math.max(dp[i][j], maxLength);
                    if (maxLength == dp[i][j]) pos = i;
                } else
                    dp[i][j] = 0;
            }
        }
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = pos - 1; i > pos - maxLength - 1; i--)
            stringBuilder.append(s.charAt(i));
        return stringBuilder.toString();

Solution 2：
最长回文字符串也有dp做法，不过复杂度也为O(2)，所以我选择选择复杂度为线性的manacher算法。manacher算法是基于由中心向两边发散的算法，所以奇偶字符串处理不同，这里采用一个小技巧，在字符串首尾，及各字符间各插入一个未出现的字符使其恒为为奇字符串。定义一个辅助数组int p[]，其中p[i]表示以 i 为中心的最长回文的半径,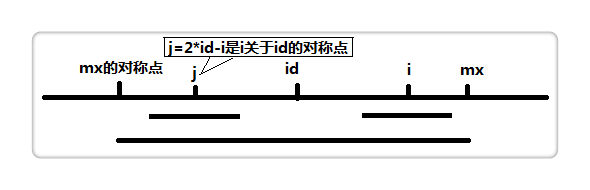

设置两个变量，mx 和 id 。mx 代表以 id 为中心的最长回文的右边界，也就是mx = id + p[id]。

假设我们现在求p[i]，也就是以 i 为中心的最长回文半径，如果i < mx，如上图，那么：

1
2
if (i < mx)  
    p[i] = min(p[2 * id - i], mx - i);

2 * id - i为 i 关于 id 的对称点，即上图的 j 点，而p[j]表示以 j 为中心的最长回文半径，因此我们可以利用p[j]来加快查找。

Code:

beat 79%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
    public String longestPalindrome(String s) {
         StringBuilder stringBuilder = new StringBuilder(s);
        stringBuilder.insert(0, "#");
        for (int i = 1; i < s.length() * 2; i = i + 2) {
            stringBuilder.insert(i + 1, "#");
        }
        String str = stringBuilder.toString();
        int mx = 0;
        int id = 0;
        int p[] = new int[str.length()];
        p[0] = 0;
        for (int i = 0; i < str.length(); i++) {
            if (i < mx)
                p[i] = Math.min(mx - i, p[2 * id - i]);
            while (i - p[i] >= 0 && i + p[i] <= str.length() - 1 && (str.charAt(i - p[i]) == str.charAt(i + p[i])))
                p[i]++;
            if (i + p[i] > mx) {
                mx = i + p[i];
                id = i;
            }
        }
        int max = 0;
        for (int i = 0; i < p.length; i++) {
            max = Math.max(max, p[i]);
            if (max == p[i])
                id = i;
        }
        stringBuilder = new StringBuilder();
        if (str.charAt(id) != '#')
            stringBuilder.append(str.charAt(id));
        for (int i = 1; i < max; i++) {
            if (str.charAt(i+id) != '#') {
                stringBuilder.append(str.charAt(i + id));
                stringBuilder.insert(0, str.charAt(i + id));
            }
        }
        return stringBuilder.toString();
    }
}
Thanks!